和微波频段的可靠的测量以及随之而来的有关可靠测量标准的要求。这便引入了用精确的同轴空气传输线作为

  的最基本的标准参考件[ 1 ] ，[ 2 ] ;见图1 。这些传输线使用了具有极高导电性的金属来作为导体材料，使用空气作为电介质，这归因于空气在射频和微波频段内简单的和可预测的电磁特性（例如，磁导率和介电常数）[ 3 ] 。这便保证了这些传输线的特性与理想传输线 ]。

  图1 一个具有不一样长度的高精度参考同轴空气传输线 年代，人们做了大量的工作来开发高精度同轴连接器以保证在微波频段所进行的测量具有非常好的重复性和可再现性[ 5 ] [ 6 ] 。为了集中精力进行这项工作，便成立了若干个委员会（包括符合IEEE 高精度同轴连接器子委员会[ 7 ] ），任务是为这些高精度连接器制定标准。在60 年代后期，具有高精度测量能力的第一台全自动

   较小尺寸的高精度同轴连接器（从3.5mm 连接器开始[10]，到1mm连接器结束[11]），使得测量可以在更宽的频段内进行

   适用于校准和/或验证VNA 性能的VNA 校准和验证工具套件

  校准技术[包括直通-反射-线 ]，线段-反射-线 ] ，等等] 由国家测量标准实验室所采用的6-端口VNA [14][ 例如美国的国家标准和技术研究院局（NIST）和英国的国家物理实验室（NPL）等]来提供一种独立的测量方法以验证商业化的VNA 的性能。

  最后，同样是在80 年代末和90 年代初，为了支持快速地发展的微电子工业，国家测量标准实验室（即NIST 和NPL 等）开始将它们的注意力转向了使用VNA 对平面电路做测量的可靠性的论证。NIST 和NPL 均生产制造了含有与同轴空气传输线等效的平面电路的标准圆芯片[15]，[16] 即高精度的共面波导段和/或微带传输线。这些传输线为进行在片测量的VNA 的校准提供了参考标准。

  然而，对于VNA 来说，校准这个词至少有两种不同的意义。首先，仍旧能采用传统的校准概念，将VNA 送出去校准，通常是每年一次。（或者，有些公司会指派校准专家前来，提供现场校准服务。）然而，与本文更贴切的是另一种在本地进行的校准方式，通常是在每次要进行一系列测量之前，在进行仪器准备和配置时进行的校准。第二种校准形式的目的是在要求的测量频率上去除来自于仪器硬件的系统误差（并且要将在特定的实验中所需加入的附件考虑进来）。例如，可能会要求是在片测量环境。在这种情况下，首先要将电缆连接到VNA 前面板的连接器上，随后是同轴适配器，最后是在片测试探头（图3 ）。第二种校准形式既要修正这些附加组件的误差，也要修正VNA 系统误差。这便是为什么将这类校准称为误差修正，本文将要讨论这种类型的校准。

  日益提高的VNA 测量精度的要求可以通过下列几个方面来达到，改善硬件性能，改进用来表示误差的模型，改进用于计算这些误差的校准方法，以及改进校准标准件。对于S -参数测量来说，系统误差是通过被称为测量系统（即VNA）的误差模型来表示的。在误差模型中所包含的误差系数的数量以及误差模型的类型取决于

  ）测量的影响。这些模型是通过采用假想的二端口误差网络而开发出来的，用来代表系统误差。它们由硫参数来描述，并且被包含在测量信号的路径中[ 8 ] 。一个反射（一端口）测量的误差模型仅仅包含一个误差网络。最初，这个网络是由含有4 个S-参数的矩阵来表示的。然而，后来发现只需要

  来进行进一步的误差修正。因此，可用3 项误差模型来代替包含有4 个S-参数的矩阵，其中系数

  （反射跟踪）（图4）[18]。今天，3 项误差模型仍然是一端口网络标准和修正过程中最常用的表示方法。

  参数）。正如在[18]中所介绍的，这样一个系统只需要5 个误差项。这便需要另外一个代表测量端口之间信号泄漏的误差项，从而将模型扩展到6 个参数（见图6）。

  8（10）项和5（6）项误差模型已经使用了近十年而未进行大的改动。[注意在这里及本文的其它地方，括号中的数字代表将泄漏项（Ex）加入后的误差项数。这些都是选择项，可能并不完全代表串音（正如在本文中进一步讨论的），因此我们未将它们加入到专业术语中。]在任何一个模型中，都要在每个测量频率上定义误差项的值，并将其存入到VNA 内存中。因此，对误差模型的扩展，包括使用附加的误差项，为不同的测量开发出一个统一的模型，从商业角度上讲还不是一个可行的选择。（在那个时候，计算器内存的成本仍然是一个主要的设计考虑因素。）

  半导体技术的快速发展极大地提高了低成本读/写存储组件以及镶嵌在测量仪器中的大容量存储设备的供货量。这便极大地增强了VNA 的误差建模能力。测量系统被统一了，与测量配置相独立的10（12）项模型被引入到商业化的VNA 中[19]（见图7）。这个误差模型成为二端口VNA 描述系统误差的标准模型。这个模型已被实施在所有现代化的测量仪器中。

  上面所讲述的和图8 所示的10 项模型是通过有效S-参数来代表系统的测量误差的。1975 年，Tektronix 公司的工程师们介绍引入了一个不同的概念[24]。他们建议用误差传输参数（T）表示的两个黑盒来描述二端口的系统测量误差（图9）。他们的模型有8 个误差项。然而，正如随后在[12]和[25]中所示，仅需7 个误差项来进行进一步的修正。为了将这种方式与老的基于S-参数的8-项误差模型相区别[8]，通常称之为7-项模型。

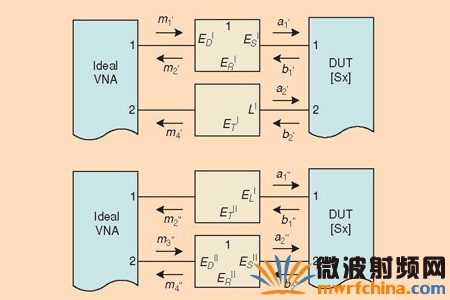
  图8 由10-项误差描述的二端口VNA 在开关的第一个状态和第二个状态时的方

  其中：m1 m4和m1“ m4”分别是正向和反向的测量值。T11 T22 定义为被测DUT 的传输参数。

  7-项误差模型和10-项误差模型均可用来描述双-反射计VNA。如果需要的线-项误差模型可以转换为10-项误差模型。已经发表了几种具有不同转换公式的方法[22]，[26] - [28]。这些公式略有不同，但都是基于相同的物理基础之上的。差别来源于作者对7-项误差模型的标示方法，例如，采用了[B]的逆矩阵。今天，这些转换技术已经在许多双-反射计VNA 中付诸实施了。

  同样试图对参考接收机类型的VNA 也使用7-项误差模型[29]。事实上，这里是假设测量装置的源匹配与负载匹配相同，而这种情况只有当测量装置的开关是理想状态时才能成立。对于一个实际的系统来说，这种假设会导致出现不能容忍的测量不准确性，特别是对具有高反射性的DUT 来说[30]。只有10-项模型才能保证对参考接收机型VNA 的完整描述。

  正如上面所提到的，甚至在VNA 的第一个误差模型中已经包含了特殊误差项，是用来描述一个系统测量端口对另一个端口的影响（即，泄漏项，Ex）。泄漏可以简单地定义为匹配完美的VNA 端口之间的传输系数。这种定义只适合那些具有与系统阻抗相同的输入和输出阻抗的DUT 的测量情况。当测量其它器件时，这种泄漏项的定义方式会降低测量的准确性。

  这个概念是1977 年由Special 和Franzen 提出的[31]。n-端口VNA 的系统测量误差是由一个2n-端口的虚拟误差网络来表示的，它的一个n-端口与DUT 相连，另一个n-端口与理想的没有误差的VNA 相连。误差网络含有(2n)2 个系数，并且描述了所有测量端口之间可能的影响。事实上，一个误差项可以设为自变量，误差模型便可以用这一项来进行归一化。即，只有4n2-1 个系数之间是线性地相互独立的。这样，这些误差项便可以完全描述这样一个系统[32]。

  4n2-1 模型只适用于建立在双-反射计概念上的VNA（有2 n 个测量接收机，图12）。然而，后来才证明参考通道VNA（有n+1 个参考接收机）的完整的误差模型也同样可以建立（图13）。这包含进了更多的误差项：例如，对一个二端口VNA 有22 个系数，而对于二端口双-反射计VNA 则只有15 个系数[33]。

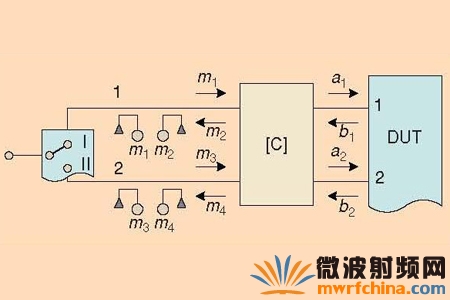
  图12 基于双-反射计结构的含有泄漏的VNA 的方框图。对二端口系统来说，矩阵[C]含有15 个误差系数。

  包含串音的误差模型能够使用更通用的形式来描述测量系统。通过将串音误差系数设为零，它们可以转化为等效的，无串音的模型。这样，22-项模型（对于一个n+1 测量接收机VNA 来说）可简化为一个（2n2+ n）的无串音模型(即，二端口10-项模型)。在2n 个测量接收机VNA（4n2-1 项模型）中忽略串音的影响，则给出了（4n-1）-项误差模型（对两端口网络来说即为7-项误差模型）。

  对于某些应用来说，多端口系统不同测量端口之间的泄漏是不同的。例如，采用双在片测量探头的（每个探头为二端口）的多端口在片级测量系统显示出在内侧（输入探头）端口之间的串音很强，而探头对探头之间的影响要小得多。针对这种情况，仅在那些对测量结果影响最大的系统模型中引入串音系数则是一个可行的方案。

  [34] 中介绍了对于4 端口测量系统的解决方案。在这种情况下，误差网络被分为两部分。每部分只包含内侧端口（例如，网络[C1]是对端口1 和2 的，另一个分开的网络[C2]是针对端口3 和4 的，见图14 所示）。这种方案因为将误差项从4n2-1 减少到2n2-1 而大大简化了对测量系统的表达，其中n 是VNA 的端口数。这样，当描述一个4 端口VNA 时，只需要31 个误差系数（对于部分泄漏模型），而不是63 个误差系数（对于完全泄漏模型）。

  网络分析仪发展的40 年历史中，已经开发了多种多样的校准方法。其中有些变成了事实上的标准方法，而其它的仅仅是改善S-参数测量精度的中间步骤。

  1971 年，kruppa 和Sodomsky 取得了重大突破[35]。第一个由8-项误差模型来明确地描述二端口VNA 的校准解决方案问世了。这个方案在每个VNA 端口上使用了三个反射标准件（开路，短路，和终端匹配）以及将两端口直接相连的标准件（直通）。通过在每个VNA 端口对开路，短路和负载的测量数据，可以定义每个端口的三个误差项S11，S22，和S12S21 （ED, Es，ER）。T21和T12 项是通过使用直通标准件分别进行正向传输和反向传输测量而计算出来的（如图5 所示）。

  针对不同的测量装置配置（误差模型），对这种显示解方法进行了进一步的改进[20] ，[21] ，最后，Hewlett-Packard 于1978 年将这个10-项误差的显示解校准方案商业化了。从那时起，这种校准过程深受欢迎，被命名为短路-开路-负载-直通（SOLT）或直通-短路-开路-匹配（TOSM）。今天，所有现代化的VNA 都实施了这种非常行之有效的SOLT 校准技术。

  SOLT 方法的精度关键取决于校准标准件的制造和建模的容许偏差（即集总参数的开路，短路和负载组件）。因为这些标准件的精度随着频率的升高而劣化，所以，要在高频下实现可靠测量仍然是一个挑战。其它的程序，如改善校准标准的模型（即，[36]，[37]）或使用参考校准的原始校准标准件[38]，可以提高SOLT 方法的精度。

  Engen 和Hoer 于1974 年提出的TRL 校准法（另一种变形是LRL）使VNA 校准理论的发展又上了一个新的台阶[12] 。这是首次出现的不要求所有标准件或者是理想的，或者其所有参数都完全已知的校准方法。通过使用测量结果的冗余性（这是双-反射计VNA 和7-项误差模型的优点），TRL 可以确定原始校准标准件的未知参数，如反射标准件的反射系数和线段标准件的传输常数。这种使用部分已知标准件来对VNA 进行校准的新原理后来被称为自校准。

  TRL 技术的另一个优点是通过使用定义明确的空气隔离线段的标准件使得实现真正的校准和测量的可追溯性成为可能。然而，TRL 会受到频率的限制。这个限制能够最终靠加入另外的线段标准件，并且对冗余测量信息进行统计分析来得到克服（与之类似的统计手段如，加权最小平方[39]和广义距离回归（generalized distance registration）[40]已被用于一端口VNA 的校准中，大大改善了整体测量精度），使得TRL 成为高精度测量的基准[41]-[43]。

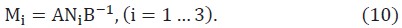
  只需从（9）中的12 个等式中解出7 个未知量的值，便可以对系统进行完整的表征[如式（6）]。这种冗余性对标准校准件提出了一般性的要求（见表1），并且有可能推导出许多不同的校准方法[25]，[44]-[46]。

   对一个已知参量进行一次测量（例如，标准件的反射系数可确定一个误差项）

   对未知参量在不同条件下进行两次测量（例如，在VNA 的两个端口对同样的一端口标准件的反射系数进行测量）能确定一个误差项。

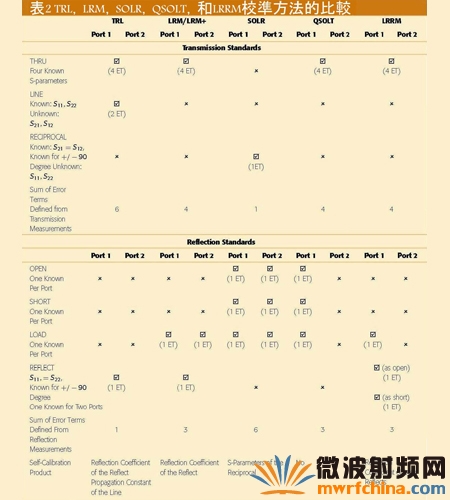
  自校准方法要求确定7 个误差项。在一般情况下，这可通过将已知和部分已知的标准件进行任意组合来得到（图15）。今天，TRL，线段-反射-匹配（LRM）[也称为直通- 反射- 匹配（TRM ）或直通- 匹配- 反射（TMR）]，短路-开路-负载-互易二端口网络（SOLR），快速-短路-开路-负载-直通（QSOLT），以及线段-反射-反射-匹配（LRRM）是最常用的覆盖了非常广泛的各种应用的自校准方法。

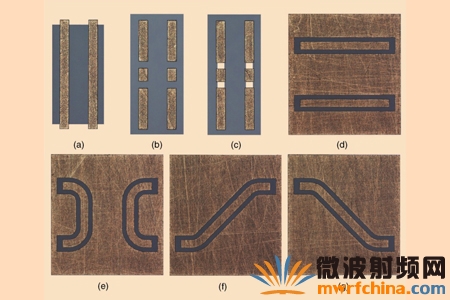
  LRM 法[47]是为解决传统TRL 中的带宽限制问题而开发的。它采用了两个一端口匹配（负载）组件来代替线段标准件（或一套不同的传输线）。从理论上说，LRM 可以被认为是一种宽带校准方法。然而，商业化的LRM只有在使用纯粹阻型，高对称性的50 负载时才能达到好的校准精度。这种要求是很难达到的，特别是在圆芯片的在片测量中。另一些更进一步的改进方案-类似于NIST [48] 的LRM 法和线段-反射-匹配，以及高级（LRM+）[49] 均是为了解决传统LRM 的这个主要缺点的。

  SOLR 法不要求知道直通标准件的所有信息[50] 。事实上，任何一个能提供对称（正向/反向）传输系数（互易）的无源二端口组件均可用于校准过程。SOLR 对于那些难以使用直通组件的测量装置是很有帮助的：例如，在同轴式应用中，当测量端口是相同性别时，或者当在圆芯片级别上采用的是矩形端口时。SOLR 法的精度从根本上取决于一端口标准件（开路，短路，负载），这些标准件要么是理想的，要么其特性是完全已知的。

  与SOLT 一样，QSOLT 方法要求所有标准件都是已知的。然而，它取消了在VNA 第二个端口对一端口标准件进行测量的要求[51]，[52]。这个特性极大地减少了对标准件进行再连接和再测量所花费的时间。然而，需要注意的是用QSOLT 法所校准的VNA 在它的第二个端口，即在校准过程中未连接一端口标准件处，存在着明显的测量误差[53]。

  LRRM 法是第一个明确地用于圆芯片级测量的方法。它是设计用来解决平面集总参数负载中诸如潜在的不对称性，阻抗与频率的相关性[54]等方面的限制的。然而，就像QSOLT 一样，它只在VNA 的一个端口对负载标准件进行测量。对于有些应用，这会导致在第二个VNA的端口处进行的测量不太可靠[55]。

  很明显，对泄露系统的校准（例如，由15-项模型所描述的）要求有大量的标准件和/或校准测量。[56]中介绍了一个15-项模型的迭代解决方法。它建议使用4 个完全已知的二端口标准件：其中一个标准件是直通件，而其它3 个标准件是匹配-匹配，开路-短路，短路-开路的组合。正如随后在[57]中所介绍的，仅采用了4 个完全已知的二端口的标准件会导致一个不确定性的方程系统，从而最终降低了校准的精度。需要至少5 个这样的标准件。

  当校准7-项误差系统时，可用不同的方法来计算所选择的误差项。例如，人们可以将SOLR 与LRM[63]或其它方法相结合进行混合校准[64]。当一些直通标准件很难表征时（例如，在圆芯片上)，就可以看出这种方法的好处了。然而，混合法在校准动态范围上可能会有些限制，这是因为它们是基于7-项模型基础之上的[65]。

  [66]和[67] 提出了另一种将不同校准方法的优点与通用的反射- 反射- 匹配- 直通相结合的思想，高级（GRRMT+）多端口解决方案。与混合校准法不同，GRRMT+校准过程使用7-项模型为基础的自校准LRM+和SOLR 过程来计算出部分已知标准件（即，反射和直通）的准确的性能参数。一旦完全知道了所有校准标准件的参数，就可通过改进的GSOLT 方法加上非理想但已知的标准件来计算误差项。因此，多端口10-项模型，多端口7-项模型和混合式方法的缺点便可一次性全部克服。

  电磁干扰，高敏感度，高数据传输速率的需求推动了高频无源和有源差分式器件的发展。因此，测量系统的改进是提供宽带差分式驱动信号的不可分割的一部分。

  第一台商业化的能进行真正的差分式测量的多端口VNA 已经出现了[68]，[69]。最近，也发表了一些修正系统误差的方法[70]，[71]。这些方法都是对现有的单端系统来进行了一些修改。校准和误差修正理论的下一大步很可能是引入真正的差分误差模型和校准标准件。新的简单明了的差分校准法将会极大地简化校准过程。它会将测量精度和对差分器件的表征提升到一个新的高度。